Coin Flip Strategy

 If a coin landed on heads 60% of the time and you are offered 1:1 odds would you play? 

Short answer, yes obviously we should play. The expected value is 20% per flip. 

EV = 0.6*x - 0.4*x = 0.2

But how much should you bet? This depends on your individual risk appetite. There is a whole area of economics dedicated to studying this known as utility theory. Economists use utility functions to quantify human preferences of different choices. Each individual aims to maximize their utility function.

This can be applied to investment decisions with respect to the risk reward trade-off. For a given level of utility there is an indifference curve that represents the tradeoff between additional risk and additional expected return. An investor can be expected to get the same satisfaction from each point on this curve. 

This is all a fancy way of saying that traditional risk measurements do not account for the subjective aspect of risk. Everyone has a different attitude towards risk and how much they are comfortable taking. So to decide how much I would  bet on this unfair coinflip:

Would I bet £5? Yes. £100? Yes. £1000? Probably not. £10000? Definitely not.

The size of the stake does not influence my probability of winning, I have a 20% edge regardless of how much I bet. However, the larger the stake becomes the more concerned I become about the loss of that money than the possibility of doubling it. This means I have a risk averse utility curve which is the same for almost all humans. Sam Bankman-Fried (in)famously had an approximately neutral appetite to risk according to Michael Lewis. His linear utility curve meant he would bet big on any positive expected value bet. I do not think this is a good approach to life and I wonder if Sam does.

How would you play a long term strategy?

Suppose this coin flip is a game we can play repeatedly, like an edge one might discover in the betting markets. What is the best way to maximize long-term return while minimizing the risk of losing our capital?

To answer this I designed a monte carlo experiment to simulate the repeated coin flip game. I defined "long-term" as 1000 flips, so if I haven't run out of money after 1000 flips the game ends. I then run this 1000 flip game 10000 times. The strategy I use is a simple one, for each coin flip I bet x% of my capital, and x remains constant for every flip. Running the experiment for different values of x I can simulate the results to obtain the best ratio of capital to use on each flip for a long term strategy. I use an x range of every 10% from 10 to 100%.

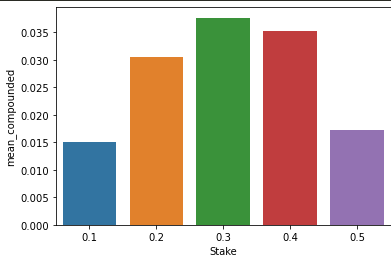
Lets look at the average return of each of these strategies. The mean return of a strategy after 1000 flips gets very high so I convert arithmetic mean to a compounded rate per flip to scale it nicer for plotting.  value of 0 signifies the mean return was negative.

We see that the highest average return comes from investing 30% of our stake on each flip, closely followed by the 40% strategy. Investing anything over 50% resulted in losing all of our money in the long run.

But this doesn't take account of the variance in returns. I calculate the standard deviation of each strategy and now represent as a sharpe ratio. We see the 10% strategy has the highest sharpe, which must be a result of relatively lower risk as we already saw it has the lowest expected return.

Given the high level of variance ivolved, it would be helpful to visualize the distribution of possible return paths. To do this I calculate the compound return of all n=10000 iterations for each strategy and create a density plot. The reason I use compound return here is for scaling purposes, so remember the x axis here is what the % return would be per flip to result in the compounding return that was observed. 

We see that despite positive expected returns, 40% and 50% strategies have a significant proportion of paths that end with losing money. The best strategies here are the 10% and 20% ones. 20% has a higher upside with marginally more risk.

Lets consider the risk of going bust in each strategy. A 10% allocation strategy goes bust 0% of the time and a 20% strategy goes bust 0.06% of the time. 

Based on this risk-reward tradeoff the best strategy for maximizing return for long term investment is to allocate 20% on each coin flip.

We can also use the Kelly Criterion to decide on a strategy. The Kelly Criterion is a formula for sizing a sequence of bets by maximizing the long-term expected value of the logarithm of wealth, which is equivalent to maximizing the long-term expected geometric growth rate. The ratio of you stake to bet is calculated as 

f = p - q/b 

where, p is the probability of winning, q is 1-p and b is proportion of your stake that you get as winnings. 

In our experiment, p = 0.6, q=0.4, b = 1.0 as odds are 1:1. This implies f = 0.6 - 0.4/1.0 = 0.2. This matches our result of the empirical analysis.